Edge Preserving

1. Bilateral filter

双边滤波算法原理及代码介绍_leonardohaig的博客-CSDN博客_联合双边滤波上采样算法原理

1.1 算法解析

值域核r,表示邻域内某点(k,l)的灰度值f(k,l)与中心点(i,j)灰度值f(i,j)的差的绝对值:
- 可以看到值域核用来表征邻域内像素的相似程度(接近程度)

$G_r(P_i-P_j)=r(i, j, k, l)=\exp \left(-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)$

空间域核d,表示邻域内某点(k,l)与中心点(i,j)的欧式距离: 这就是高斯滤波核

$G_s(x_i-x_j)=d(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}\right)$

权重系数为空间域核和值域核的乘积:

$\begin{gathered} w(i, j, k, l)=d(i, j, k, l) * r(i, j, k, l)= \\ \exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right) \end{gathered}$

双边滤波中(i,j)位置的像素值g(i,j)依赖于邻域内像素值f与其权重w的加权组合(k,l表示邻域像素位置)：

$g(i, j)=\frac{\sum_{k, l} f(k, l) w(i, j, k, l)}{\sum_{k, l} w(i, j, k, l)}$

对于高斯滤波，离中心像素距离越近，权重越大（物理距离）
对于值域滤波，灰度值相差大的点权重越小，所以最终边缘交界处的权重接近于零，而非边缘处，由于灰度值相差小，所以权重较大，不可能为边缘。
当两者相乘，最终可以做到既消除噪音，又巧妙保留了边缘。

1.2 算法案例

其可以看作是10×10的一张图像，图中的数字表示每个点的像素值。在图中存在一个5×5大小的滑动窗口，我们需要求出中心点灰度值146的新像素值。
1. 边缘复制/边界填充(不多说)
2. 首先遍历整个窗口，第一个遍历到的点是165，那么中心点与该点的空间域计算结果为：
1. 再计算中心点与该点的像素域结果：

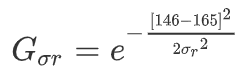
当σs=5与σr=20时，Gσs = 0.8521，Gσr = 0.6368。

3. 接着遍历整个窗口，将窗口内每个像素点都与中心点建立联系，求出它们的Gσs与Gσr的值，将Gσs与Gσr 相乘即得到每个点对应的权重Wp，即Wp = Gσs × Gσr。

在遍历结束后，用每个点的Wp乘上该点的像素值I(i,j)，并求和，这是作为分子。将每个点的Wp相加，作为分母，两者相除，即得到需要的新输出图像的中心点（i，j）的像素值。

1.3 opencv 代码实现

CV_EXPORTS_W void bilateralFilter( InputArray src, OutputArray dst, int d,
                                   double sigmaColor, double sigmaSpace,
                                   int borderType = BORDER_DEFAULT );

//第一个参数，InputArray类型的src，输入图像，即源图像，需要为8位或者浮点型单通道、三通道的图像。
//第二个参数，OutputArray类型的dst，即目标图像，需要和源图片有一样的尺寸和类型。
//第三个参数，int类型的d，表示在过滤过程中每个像素邻域的直径。如果这个值我们设其为非正数，那么OpenCV会从第五个参数sigmaSpace来计算出它来。
//第四个参数，double类型的sigmaColor，颜色空间滤波器的sigma值。这个参数的值越大，就表明该像素邻域内有更宽广的颜色会被混合到一起，产生较大的半相等颜色区域。
//第五个参数，double类型的sigmaSpace坐标空间中滤波器的sigma值，坐标空间的标注方差。他的数值越大，意味着越远的像素会相互影响，从而使更大的区域足够相似的颜色获取相同的颜色。当d>0，d指定了邻域大小且与sigmaSpace无关。否则，d正比于sigmaSpace。
//第六个参数，int类型的borderType，用于推断图像外部像素的某种边界模式。注意它有默认值BORDER_DEFAULT。

2. Joint Bilateral filter

联合双边滤波器（joint bilateral filter)【OpenCV】_ShaderJoy 的兴趣技术杂货铺-CSDN博客

2.1 简介

前面介绍了双边滤波器（bilateral filter,LBF），然而BF的权值是不稳定的，因此在边缘附近会出现一些翻转。此外BF计算复杂度是O(r^2)；为了改善BF权值的稳定性，引入了联合双边滤波器（joint bilateral filter ,LBF)。两者之间的差别就是JBF用了一个导向图作为值域权重的计算依据。下面我们通过数学公式展示二者的不同：
先看BF的，如（1）所示，

$J_{p}=\frac{1}{k_{p}} \sum_{g \in \Omega} I_{q} f(\|p-q\|) g\left(\left\|I_{p}-I_{q}\right\|\right),$

再次解释一下公式中的符号意义，其中I表示输入图像，p、q表示像素在图像中的坐标，Ip表示对应位置的像素值，J表示输出， f、g是权重分布函数，一般为高斯函数。这种滤波的结果就是周边像素的权值不仅和距离有关还和那个位置的像素值有关。

再看JBF，如（2）所示，

$J_{p}=\frac{1}{k_{p}} \sum_{a \in 0} I_{q} f(\|p-q\|) g\left(\left\|\tilde{I}_{p}-\tilde{I}_{q}\right\|\right)$

如果在值域的权重计算过程引入另外一幅图像，如下式，则称之为联合双边滤波。 $\tilde{I}$ 就是引入的另外一幅图像。该图像必须与待处理的图像相似。
联合双边滤波上采样技术也很简单，一种便于理解的也便于写代码的方式就是把下采样并进行处理过后的小图按照最近邻插值的方式放大到原图大小，然后再用原图的数据和这个放大的结果进行联合双边滤波处理。

2.2 代码实现：

function B = jbfltGray(D,C,w,sigma_d,sigma_r)
%    D should be a double precision matrix of size NxMx1 (i.e., grayscale)  with normalized values in the 
%    closed interval [0,1]. 
%    C should be similar to D, from which the weights are calculated, with normalized values in the
%   closed interval [0,1]. 
% Pre-compute Gaussian distance weights.
[X,Y] = meshgrid(-w:w,-w:w);
G = exp(-(X.^2+Y.^2)/(2*sigma_d^2));
% Apply bilateral filter.
dim = size(D);
B = zeros(dim);
for i = 1:dim(1)
   for j = 1:dim(2)      
         % Extract local region.
         iMin = max(i-w,1);
         iMax = min(i+w,dim(1));
         jMin = max(j-w,1);
         jMax = min(j+w,dim(2));
         I = D(iMin:iMax,jMin:jMax); 
         % To compute weights from the color image
         J = C(iMin:iMax,jMin:jMax);
         % Compute Gaussian intensity weights according to the color image
         H = exp(-(J-C(i,j)).^2/(2*sigma_r^2));
         % Calculate bilateral filter response.
         F = H.*G((iMin:iMax)-i+w+1,(jMin:jMax)-j+w+1);
         B(i,j) = sum(F(:).*I(:))/sum(F(:));   
   end
end

OpenCV 3.x.x的扩展模块（ximgproc. Extended Image Processing）也添加了JBF的 API ：


#include "stdafx.h"
#include <opencv2/opencv.hpp>
#include <ximgproc.hpp>
 
int main()
{
	cv::Mat src = cv::imread("data/dp.png", 1); // 原始带噪声的深度图
	cv::Mat joint = cv::imread("data/teddy.png", 0);
 
	cv::Mat dst;
	int64 begin = cvGetTickCount();
	cv::ximgproc::jointBilateralFilter(joint, src, dst, -1, 3, 9);
	int64 end = cvGetTickCount();
 
	float time = (end - begin) / (cvGetTickFrequency() * 1000.);
	printf("time = %fms\n", time);
 
	imshow("src", src);
	imshow("joint", joint);
	imshow("jointBilateralFilter", dst);
	cv::waitKey(0);
 
 
    return 0;
}

2.3 效果

2.4 评价

Advantages：

Preserve edges in the smoothing process 可以在平滑处理后仍保留边缘
Simple and intuitive 简单直观

Problems：

Complexity
- Brute force: $O(r^2)$
- Distributive histogram: $O(log r)$
- Integral histogram: $O(1)$
Gradient distortion: 梯度翻转
- Preserves edges, but not gradients
- 由于高斯滤波对边缘敏感，容易对边缘部分的像素值造成很大的变化，这就导致边缘部分可能有梯度翻转的现象

3. Guided filter

3.1 算法解析

这里要说的引导滤波，某像素点的输出结果为：

$q_{i}=a_{k} I_{i}+b_{k}, \forall i \in \omega_{k}$

其中，q 为输出图像，I 为引导图像，a 和 b 是当窗口中心位于 k 时该线性函数的不变系数。对于给定k个窗口，我们可以假设对于k个窗口覆盖到引导图像的每个像素都和输出图像对应的像素点有一个线性映射的关系，其中对于每一个窗口，其线性的参数是是一样的。
$n_i$为噪声，p是q受到噪声n污染的退化图像

$n_i = p_i-q_i$

价值函数如下：

$E\left(a_{k}, b_{k}\right)=\sum_{i \in \omega_{k}}\left(\left(a_{k} I_{i}+b_{k}-p_{i}\right)^{2}+\varepsilon a_{k}^{2}\right)$

即：

$\min _{(a, b)} \sum_{i}\left(a I_{i}+b-p_{i}\right)^{2}+\varepsilon a^{2}$

第二项为正则项，用于限制a的大小，$\epsilon$为超参。类似于最下二乘法求解，式（9）的解为：

$\begin{aligned} a_{k} &=\frac{\frac{1}{|\omega|} \sum_{i \in \omega_{k}} I_{i} p_{i}-\mu_{k} \bar{p}_{k}}{\sigma_{k}^{2}+\varepsilon } \end{aligned}$ $\begin{aligned} b_{k} &=\bar{p}_{k}-a_{k} \mu_{k} \end{aligned}$

这里的$p_i$指的是对于原图像对应的第$i$个像素，$\mu_k$表示对应第k个窗口引导图像的所有像素值的均值，$\bar{p_k}$指的是对于该窗口覆盖原图像所有像素的均值，$\sigma^2_k$指的是对于第k个窗口引导图像上像素值的方差，$\varepsilon$是超参。
最后取均值可以得到式（7）的结果为：

$\begin{aligned} q_{i} &=\frac{1}{|\omega|} \sum_{k: i \in \omega_{k} \ldots t_{p i a 0 x u e}}\left(a_{k} I_{i}+b_{k}\right) \\ &=\bar{a}_{i} I_{i}+\bar{b}_{i} \end{aligned}$

其中，$\bar{a}_{i}=\frac{1}{|\omega|} \sum_{k \in \omega_{i} } a_{k}, \bar{b}_{i}=\frac{1}{|\omega|} \sum_{k \in \omega_{i}} b_{k}$，其物理含义是对于经过第$i$个像素的所有窗口对$a_k, b_k$进行平均。
即：

$\begin{aligned} a_{k} &=\frac{\operatorname{cov}_{k}(I, p)}{\operatorname{var}_{k}(I)+\varepsilon} \\ b_{k} &=\bar{p}_{k}-a \bar{I}_{k} \\ q_{i} &=\frac{1}{|\omega|} \sum_{k \mid \in \omega_{k}}\left(a_{k} I_{i}+b_{k}\right) \\ &=\bar{a}_{i} I_{i}+\bar{b}_{i} \end{aligned}$

3.2 总结

总结：导引图像I与 q 之间存在线性关系，这样设定可以使导引图像提供的信息主要用于指示哪些是边缘。如果导引图告诉我们这里是边缘，最终的结果就设法保留这些边缘信息。所以，引导滤波的前提条件是：当I和q满足线性关系才有意义。

其最终结果可以理解为，对于每个输出的像素为：对引导图像对应的像素的一个变换的均值。
对于第k个经过该像素的窗口，我们可以得到对应的一个线性变换，从而得到对应的输出像素值；
遍历这么多个窗口的变换后，我们在求一个均值，最终就会得到我们想要的答案
这里的$\bar{a_i}$和$\bar{b_i}$可以理解为经过第$i$个像素窗口的系数的均值

3.3 为何可行

3.3.1 Def

即：

$\begin{aligned} a &=\frac{\operatorname{cov}(I, p)}{\operatorname{var}(I)+\varepsilon} \\ b &=\bar{p}-a \bar{I} \end{aligned}$

$\varepsilon$可以视为边缘保留程度的评判

3.3.2 Smoothing

其意义是，如果要对图像进行平滑处理，只需增大$\varepsilon$，这样就会使得都$\begin{gathered}
a \approx 0 , b \approx \bar{p} \end{gathered}$ 则输出图像的像素近似为高斯过滤后的输出图像，或者说此时由于是非边缘处，所以变化很小，方差和卷积自然很小，会远小于一个阈值，这个阈值就是$\varepsilon$。
对于$\bar{p}_k$指的是对于第k个窗口在原图像覆盖的所有像素值的均值，$\overline{\bar{p}}$则为对于这样k个窗口得出的$\bar{p}_k$的均值化，其实结果就相当于做了滤波。

3.3.3 edge-preserving

由于$\bar{a}$和$\bar{b}$是常数，所以求梯度是零，这里表示了对于输出图像每一个像素的梯度值可以理解为引导图像梯度值的增益或者衰落。
在这里，也说明了超参$\varepsilon$可以控制a的大小，从而控制输出图像的像素值梯度，我们知道边缘处的像素值梯度会明显大于周围，这就意味着超参实质是在增强输出图像的边缘

我们可以发现，$\varepsilon$越小，边缘越明显，当然越大，则越模糊。

3.4 与BF对比

由于引导图像和输出图像的梯度值具有线性关系，所以不会在边缘处出现梯度翻转的现象，相反，其会对边缘处进行增益。